Modelling the Betting Market
With Beta Regression
If you’re attempting to predict the results of cycling races, it’s crucial to utilize any piece of information you have. In my own models, I’m leveraging data about riders (estimated weight, past performances on different terrains, estimated power data), the parcours (how flat/hilly/mountainous, whether the race is likely to end in a bunch sprint), team tactics (how likely the breakaway is to win, who is likely to be a protected leader), and weather (temperature mostly).
All of that data combined together in an intelligent way can give you strong insight into who is likely to win on the day. This way of analyzing a race can be looked at as the bottom-up approach; take a bunch of factors which could impact the result, combine intelligently, and see what sifts out. Today I want to discuss another way of approaching the problem which can be considered a top-down approach: using past betting market prices to guide you.
Over the past five years, I’ve gathered pre-race odds for almost 1,000 stages/races from the top level of men’s cycling from providers like Bet365, Unibet, Betway, and others. These pre-race market prices are influenced and sharpened by savvy bettors (though certainly not to the extent of eg the NFL or Premier League given the huge amounts bet on those competitions relative to cycling). As such, the prices before a race kicks off are a strong indicator of who oddsmakers and sharp cycling punters think will succeed considering all of the factors I discussed above (performance, parcours, weather, tactics, etc) and others.
We can leverage this data to make inferences about how the market views certain riders, where the market sees them as likely to perform well, and who is trending up or down in form. The market will also likely respond quicker to jumps or drops in form than a machine learning model as it is being shaped day-by-day by the opinions of hundreds of punters who watch and analyze the races.
How to model this data
First we need to convert data which is in decimal odds format with margin applied to data which is in probabilities without margin (100% price). Converting decimal odds to implied prices is as easy as dividing 1 by the price (eg, 6.5 = 1/6.5 = 15.4%). There are several useful approaches to removing margin from betting market prices; check the implied package for some of them. I use the power method which adjusts the implied price using an exponent (eg, 15.4% ^ (1/k)) and then optimizes that exponent over all prices to find the correct value for k.
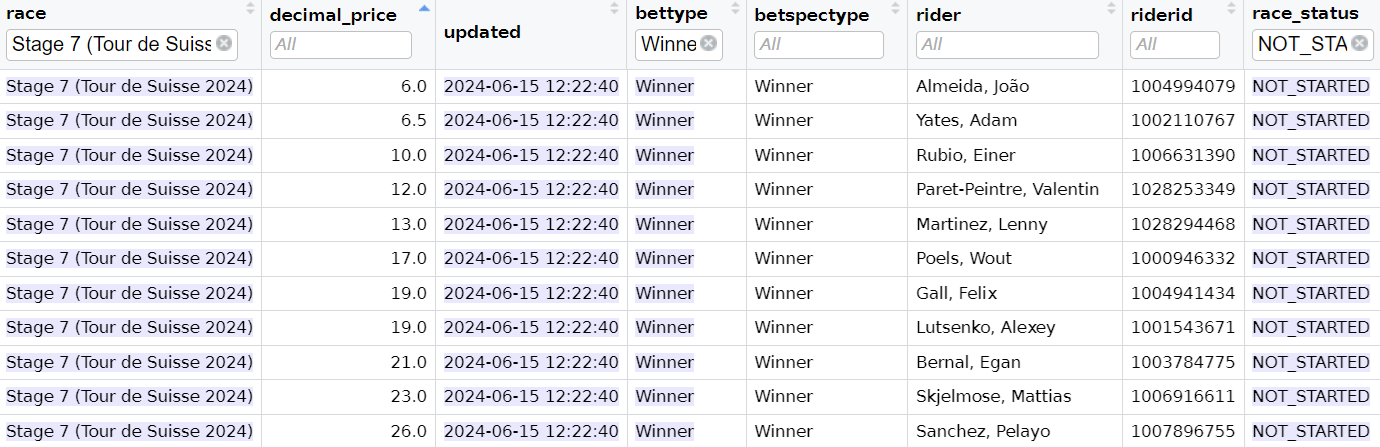
This is an example of the top of the market for Tour de Suisse stage 7 last week. Almeida and Adam Yates were significant favorites at 6.0 and 6.5 followed by Rubio, Paret-Peintre, Martinez, and others. When we account for margin, Almeida and Yates come out to around 12% and around 10% to win. Repeat for all 1,000 races and now we have the market’s best estimate of a rider’s likelihood to win the race.
We now need to consider how to model this data. In the past, I’ve modelled data like finishing position using mixed effects linear regression. This approach essentially finds the individual rider-level impacts of various factors on their finishing position. For example, a model which considers the climbing difficulty of a race and whether it ended in a bunch sprint to model a rider’s finishing position will likely have very negative intercepts for riders like Vingegaard and Philipsen (as both finish highly in races), but have a negative slope for climbing difficulty for Vingegaard and positive for Philipsen (as Vingegaard finishes better on races with a lot of climbing and Philipsen finishes worse. Vice versa, the bunch sprint variable will likely be very negative for Philipsen as he cleans up bunch sprints, while being positive for Vingegaard as he does not.1
Such an approach can also be leveraged to model these betting market prices. We can use the same information (climbing difficulty, bunch sprint or not) to find rider-level impacts on likelihood of winning the race.
However, modelling probabilities is very tricky using linear regression. Linear regression can often produce coefficients that lead to negative predicted probabilities or probabilities predicted over 100%. Indeed, a linear version of the model I’ve laid out above sets the intercept term (basically, how good is this rider in general without controlling for climbing difficulty or bunch sprint finish) as a negative value for three quarters of all riders. Sprinter Sam Bennett is predicted to be -16% to win a high mountain stage while climber Tao Geoghegan Hart is -0.5% to win a bunch sprint stage. Obviously neither of those is possible.
Instead of modelling this using linear regression, I settled on a beta regression. Beta regression is perfect for modelling any continuous data which is bounded by 0 to 1 which is exactly what probability data is. The glmmTMB package is specifically designed to fit mixed effects models using a range of non-normal distributions.
After deciding on a framework for the model, I also chose to include two other variables:
First, the strength of peloton to penalize high probabilities in weak races and boost low probabilities in strong races
Second, a variable meant to identify the impact on rider’s probabilities of races that are very likely to be contested by the top riders (essentially first days of Grand Tours and one day races) versus potentially not controlled (Grand Tour breakaway days). If the market suspects that a certain race will be punted by top riders to a breakaway and adjusts prices accordingly, we don’t want to penalize those top riders. On the flip-side, we want to sharpen our estimate of a rider’s probability to win using races where the top riders will certainly be contesting the win.
Results
The coefficients outputs are harder to interpret as they must be converted, but we can see who the model considers as the top 10 riders based on the betting market’s opinion. Perhaps only Matej Mohoric is a surprise, but he’s closely followed by Pidcock and Adam Yates - and Mohoric does win often. Jonas, Pogacar, and Carapaz are the riders most positively influenced by tough climbing day, while Bennett, Philipsen, and Mads Pedersen are hurt the most. Groenewegen, Bauhaus, and Jakobsen are the most helped by a bunch sprint finish.
Pogacar, Van Der Poel, and Christophe Laporte are most positively impacted by the one day race/stage 1 of Grand Tour variable. We can immediately see the limitation this variable has; Laporte is indeed a strong rider in one day race, but he will certainly not be the Visma-LAB leader for stage 1 (even if the parcours suited him better). Pello Bilbao, Mohoric, and Michael Matthews are seen as riders hurt by this variable; generally we’d expect riders who gain their success in week long stage races or breakaway days to be hurt by this variable.
Applying to Tour de France Stage 1
Stage 1 of Tour de France is a long (206 km) medium mountain day (3800 vertical meters in 7 categorized climbs) with a ~25km downhill/flat run-in to the finish. In short, it’s definitely going to be a selective day for climbers/puncheurs, but probably not something that will end in a solo unless someone absolutely flies up the final climb and group 2 syndrome bites on the run-in.
Applying that context to the model, we can output predictions for stage 1.
Pogacar is the massive favorite at about 4.3 (or about 7-2 or +350).
Mathieu Van Der Poel leads a host of the second favorites between 17.0 and 23.0 including Roglic and Remco - two of the main GC favorites. The final GC favorite Vinegaard is 6th favorite but only at 33.0.
Van Der Poel is given credit by the model for his typical very strong odds in races where the top riders will be competing for the win, but he’s the most impacted by the climbing difficulty of these top riders and if we were to ratchet up the climbing difficulty slightly, his price would cut in half quickly.
Limitations
This approach is just a tool in the tool box of pricing up who is likely to win a race. Among other things it ignores:
actual results; this model doesn’t know Alberto Bettiol just won the Italian National Championships last week which is a main reason he’s 3rd favorite in actual market
races which weren’t priced by the market; many cycling races below World Tour level are simply not priced by any of the bookmakers I track. 6th favorite Maxim Van Gils was surely highly rated to win the Grosser Preis des Kantons Aargau a few weeks ago, but I didn’t manage to find a market for that race
Past Grand Tour Stage 1s
As a bonus, this is how the six road race Grand Tour Stage 1s have played out in the last six years.
2024 Giro d’Italia: Pogacar was 1.75 favorite; Narvaez won at 23.0
2023 Tour de France: Pogacar was 3.0 favorite with Van Der Poel (5.0) and Van Aert (6.5) next favorites; Adam Yates won at 81.0
2022 Giro d’Italia: Van Der Poel was 2.5 favorite over Girmay (5.0) and Ewan (7.0). Van Der Poel won
2021 Tour de France: Van Der Poel (2.75), Van Aert (6.5), and Alaphillipe (7.0) were favorites. Alaphillipe won
2020 Vuelta: Roglic was 2.75 favorite with Valverde (5.5) second favorite; Roglic won
2020 Tour de France: Ewan (3.15) and Bennett (3.25) were favorites trailed by Nizzolo (8.5) and Van Aert (10.0); Kristoff (41.0) won in a crash marred stage
A nice mix of a significant surprise in Adam Yates, outsiders in Narvaez and Kristoff, and massive favorites winning.
These impacts are reversed from what would be intuitive because I’m modelling rank data where a negative impact predicts a better rank




Fantastically explained. I just wonder how hard they will go on the climbs and whether that results in those with a higher finishing speed having more of a chance, Slightly stronger on Van Aert, Pidcock etc. But hard to disagree with much.